simpson and their mathmatical

simpson and their mathmatical

In his BOOK simpson and their mathmatical ,The writer and physicist Simon Singh tries to explore the episodes of the cartoon series The Simpsons, searching for mathematical examples hidden in the episodes

For example, in the episode of marge and homer turna couple play, which are subject in 2006, in the last scene in the episode we see words and numbers in that snapshot, no one paid attention to it, but simon singh paid attention to it and began looking at those numbers that may appear to you at first sight It's random. That snapshot is a board stadium that says:

How many audiences are there today: 8191, 8128, 8208, No way to tell

It may seem to you that these numbers are normal or random, but the simpsons writers, many of whom have a maths background or a mathematical orientation, were touching them to write these particular numbers.

• The first number 8191 is the mersenne prime number, which is a number of initial mersenne numbers, on which the complex mathematical system is based, and it is the basis of the coding system in the world, and it establishes strong protection systems used in banks, emails and smartphones

Mersenne prime number, in number theory, a prime number of the form 2n − 1 where n is a natural number. These primes are a subset of the Mersenne numbers, Mn.

• The second number 8128 is called PERFECT NUMBER, this number is unique because DIVISORS this number when they are all combined together we get the same number

Example number 6: The divisors of number 6 are 1, 2, and 3. When they are combined, we get the number 6, so the number 6 is the perfect number.
The perfect number that follows 6 is 28, after it 496, which is followed by 8128, and after them they decrease a lot and are far apart
So much so that the French philosopher and mathematician René Descartes says that such ideal numbers are so rare  ( they are so rare!)

where 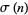 is the divisor function (i.e., the sum of divisors of  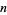including  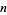itself). For example, the first few perfect numbers are 6, 28, 496, 8128, ... (OEIS A000396),since

6=1+2+3      

28=1+2+4+7+14

496=1+2+4+8+16+31+62+124+248

Perfect numbers were deemed to have important numerological properties by the ancients, and were extensively studied by the Greeks, including Euclid.

• The last number 8208 is the number of Narcissism numbers, which is equal to the sum of the numbers raised by the exponent of the number of numbers that make up the number 

Narcissist number, Armstrong number, or whole number digitally or ideally fixed plus plus number: n is a number whose sum of numbers is raised to n separately.

The first few are given by 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, 54748, ... (OEIS A005188).

Thank you for your support, and I hope you enjoy the content and benefit from it